Introduction of Set theory

A Set is an unordered collection of objects, known as elements or members of the set.

An element ‘a’ belong to a set A can be written as ‘a ∈ A’,  ‘a ∉ A’ denotes that a is not an element of the set A.

Representation of a Set

A set can be represented by various methods. 3 common methods used for representing set:

1. Statement form.

2. Roaster form or tabular form method.

3. Set Builder method.

Statement form

In this representation, the well-defined description of the elements of the set is given. Below are some examples of the same.

1. The set of all even number less than 10.

2. The set of the number less than 10 and more than 1.

Roster form

In this representation, elements are listed within the pair of brackets {} and are separated by commas. Below are two examples.

1. Let N is the set of natural numbers less than 5.

N = { 1 , 2 , 3, 4 }.

2. The set of all vowels in the English alphabet.

V = { a , e , i , o , u }.

Set builder form

In Set-builder set is described by a property that its member must satisfy.

1. {x : x is even number divisible by 6 and less than 100}.

2. {x : x is natural number less than 10}.

Equal sets

Two sets are said to be equal if both have same elements. For example A = {1, 3, 9, 7} and B = {3, 1, 7, 9} are equal sets.

NOTE: Order of elements of a set doesn’t matter.

Subset

A set A is said to be subset of another set B if and only if every element of set A is also a part of other set B.

Denoted by ‘⊆‘.

‘A ⊆ B ‘ denotes A is a subset of B.

To prove A is the subset of B, we need to simply show that if x belongs to A then x also belongs to B.

To prove A is not a subset of B, we need to find out one element which is part of set A but not belong to set B.

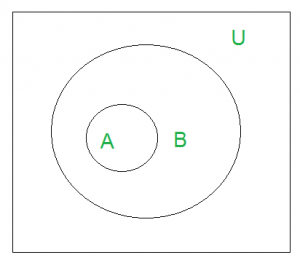
‘U’ denotes the universal set.

Above Venn Diagram shows that A is a subset of B.

Size of a Set

Size of a set can be finite or infinite.

For example

Finite set: Set of natural numbers less than 100.




Infinite set: Set of real numbers.

Size of the set S is known as Cardinality number, denoted as |S|.

Example: Let A be a set of odd positive integers less than 10.

Solution : A = {1,3,5,7,9}, Cardinality of the set is 5, i.e.,|A| = 5.

Note: Cardinality of a null set is 0.

Power Sets

The power set is the set all possible subset of the set S. Denoted by P(S).

Example: What is the power set of {0,1,2}?

Solution: All possible subsets

{∅}, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}.

Note: Empty set and set itself is also the member of this set of subsets.

Cardinality of power set is

, where n is the number of elements in a set.

Cartesian Products

Let A and B be two sets. Cartesian product of A and B is denoted by A × B, is the set of all ordered pairs (a,b), where a belong to A and b belong to B.

A × B = {(a, b) | a ∈ A ∧ b ∈ B}.

Example 1. What is Cartesian product of A = {1,2} and B = {p, q, r}.

Solution : A × B ={(1, p), (1, q), (1, r), (2, p), (2, q), (2, r) };

The cardinality of A × B  is N*M, where N is the Cardinality of A and M is the cardinality of B.

Note: A × B is not the same as B × A.

Union

Union of the sets A and B, denoted by A ∪ B, is the set of distinct element belongs to set A or set B, or both.

Above is the Venn Diagram of A U B.

Example : Find the union of A = {2, 3, 4} and B = {3, 4, 5};

Solution : A ∪ B = {2, 3, 4, 5}.

Intersection

The intersection of the sets A and B, denoted by A ∩ B, is the set of elements belongs to both A and B i.e. set of the common element in A and B.

Above is the Venn Diagram of A ∩ B.

Example: Consider the previous sets A and B. Find out A ∩ B.

Solution : A ∩ B = {3, 4}.

Disjoint

Two sets are said to be disjoint if their intersection is the empty set .i.e sets have no common elements.

Above is the Venn Diagram of A disjoint B.

For Example

Let A = {1, 3, 5, 7, 9} and B = { 2, 4 ,6 , 8} .

A and B are disjoint set both of them have no common elements.

Set Difference

Difference between sets is denoted by ‘A – B’, is the set containing elements of set A but not in B. i.e all elements of A except the element of B.

Above is the Venn Diagram of A-B.

Complement

Complement of a set A, denoted by

, is the set of all the elements except A. Complement of the set A is U – A.

Above is the Venn Diagram of Ac

Formula:
1. 


2. 

Properties of Union and Intersection of sets:
1. Associative Properties: A ∪ (B ∪ C) = (A ∪ B) ∪ C and A ∩ (B ∩ C) = (A ∩ B) ∩ C
2. Commutative Properties: A ∪ B = B ∪ A and A ∩ B = B ∩ A
3. Identity Property for Union: A ∪ φ = A
4. Intersection Property of the Empty Set: A ∩ φ = φ
5. Distributive Properties: A ∪(B ∩ C) = (A ∪ B) ∩ (A ∪ C) similarly for intersection.


Example : Let A = {0, 2, 4, 6, 8} , B = {0, 1, 2, 3, 4} and C = {0, 3, 6, 9}. What are A ∪ B ∪ C and A ∩ B ∩ C ?
Solution: Set A ∪ B &cup C contains elements which are present in at least one of A, B, and C.
A ∪ B ∪ C = {0, 1, 2, 3, 4, 6, 8, 9}.


Set A ∩ B ∩ C contains an element which is present in all the sets A, B and C .i.e { 0 }.




Power Set and its Properties




For a given set S, Power set P(S) or 2^S represents the set containing all possible subsets of S as its elements. For example,
S = {1, 2, 3}
P(S) = {ɸ, {1}, {2}, {3} {1,2}, {1,3}, {2,3}, {1,2,3}}

Number of Elements in Power Set –
For a given set S with n elements, number of elements in P(S) is 2^n. As each element has two possibilities (present or absent}, possible subsets are 2×2×2.. n times = 2^n. Therefore, power set contains 2^n elements.
Note : -
• Power set of a finite set is finite.
• Set S is an element of power set of S which can be written as S ɛ P(S).
• Empty Set ɸ is an element of power set of S which can be written as ɸ ɛ P(S).
• Empty set ɸ is subset of power set of S which can be written as ɸ ⊂ P(S).
Countable set and its power set –
A set is called countable when its element can be counted. A countable set can be finite or infinite.
For example, set S1 = {a, e, i, o, u} representing vowels is a countably finite set. However, S2 = {1, 2, 3……} representing set of natural numbers is a countably infinite set.
Note –
• Power set of countably finite set is finite and hence countable.
  For example, set S1 representing vowels has 5 elements and its power set contains 2^5 = 32 elements. Therefore, it is finite and hence countable.
• Power set of countably infinite set is uncountable.
  For example, set S2 representing set of natural numbers is countably infinite. However, its power set is uncountable.
Uncountable set and its power set –
A set is called uncountable when its element can’t be counted. An uncountable set can be always infinite.
For example, set S3 containing all fractional numbers between 1 and 10 is uncountable.
Note –
• Power set of uncountable set is always uncountable.
  For example, set S3 representing all fractional numbers between 1 and 10 is uncountable. Therefore, power set of uncountable set is also uncountable.
References

https://en.wikipedia.org/wiki/Cartesian_product

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above