Net

Inclusion-Exclusion and its various Applications

Masthai
by Masthai October 05, 2019

Inclusion-Exclusion and its various Applications


In the field of Combinatorics, it is a counting method used to compute the cardinality of the union set. According to basic Inclusion-Exclusion principle:
  • For 2 finite sets A_1 and A_2, which are subsets of Universal set, then (A_1-A_2), (A_2-A_1) and (A_1\bigcap A_2) are disjoint sets.
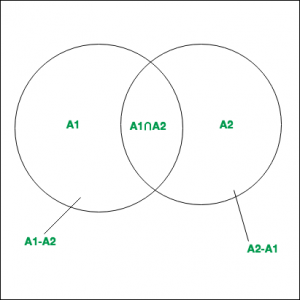    Hence it can be said that,
    \left|(A_1-A_2)\bigcup(A_2-A_1)\bigcup(A_1\bigcap A_2)\right| = \left|A_1\right| - \left|A_1\bigcap A_2\right| + \left|A_2\right| - \left|A_1\bigcap A_2\right| + \left|A_1\bigcap A_2\right|
    • \left|A_1 \bigcup A_2\right| = \left|A_1\right| + \left|A_2\right| -\left|A_1 \bigcap A_2\right|.
    • Similarily for 3 finite sets A_1, A_2 and A_3,
      \left|A_1 \bigcup A_2 \bigcup A_3\right| = \left|A_1\right| + \left|A_2\right| + \left|A_3\right| - \left|A_1 \bigcap A_2\right| - \left|A_2 \bigcap A_3\right| - \left|A_1 \bigcap A_3\right|+ \left|A_1 \bigcap A_2 \bigcap A_3\right|

    Principle :

    Inclusion-Exclusion principle says that for any number of finite sets A_1, A_2, A_3... A_i, Union of the sets is given by = Sum of sizes of all single sets – Sum of all 2-set intersections + Sum of all the 3-set intersections – Sum of all 4-set intersections .. + (-1)^{i+1} Sum of all the i-set intersections.
    In general it can be said that,
    \left|A_1 \bigcup A_2 \bigcup A_3 .. \bigcup A_i\right| = \sum\limits_{1 \leq k \leq i} \left|A_k\right| + (-1)\sum\limits_{1 \leq k_1 \textless k_2 \leq i} \left|A_{k_1} \bigcap A_{k_2}\right| + (-1)^2\sum\limits_{1 \leq k_1 \textless k_2 \textless k_3 \leq i} \left|A_{k_1} \bigcap A_{k_2} \bigcap A_{k_3}\right| .. + (-1)^{i+1}\sum\limits_{1 \leq k_1 \textless k_2 \textless k_3 \textless .. k_i\leq i} \left|A_{k_1} \bigcap A_{k_2} \bigcap A_{k_3} ..\bigcap A_{k_i}\right|
    Properties :
    1. Computes the total number of elements that satisfy at least one of several properties.
    2. It prevents the problem of double counting.
    Example 1:
    As shown in the diagram, 3 finite sets A, B and C with their corresponding values are given. Compute \left|A \bigcup B \bigcup C\right|.

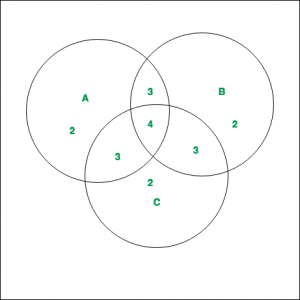
    Solution :
    The values of the corresponding regions, as can be noted from the diagram are –
    \left|A\right| = 2, \left|B\right| = 2, \left|C\right| = 2, \left|A \bigcap B\right| = 3, \left|B \bigcap C\right| = 3,
    \left|A \bigcap C\right| = 3, \left|A \bigcap B \bigcap C\right| = 4
    By applying Inclusion-Exclusion principle,
    \left|A_1 \bigcup A_2 \bigcup A_3\right| = \left|A_1\right| + \left|A_2\right| + \left|A_3\right| - \left|A_1 \bigcap A_2\right| - \left|A_2 \bigcap A_3\right| - \left|A_1 \bigcap A_3\right|+ \left|A_1 \bigcap A_2 \bigcap A_3\right|
    \left|A_1 \bigcup A_2 \bigcup A_3\right| = 2 + 2 + 2 - 3 - 3 - 3 + 4 = 1

    Applications :

    • Derangements
      To determine the number of derangements( or permutations) of n objects such that no object is in its original position (like Hat-check problem).
      As an example we can consider the derangements of the number in the following cases:
      For i = 1, the total number of derangements is 0.
      For i = 2, the total number of derangements is 1. This is 2 1.
      For i = 3, the total number of derangements is 2. These are 2 3 1 and 3 2 1.
      • Applying the Inclusion-Exclusion principle to i general events A_1, A_2, A_3... A_i and rearranging we get the formula,
      P(\left|\bigcup\limits_{k=0}^i A_i\right|) = P(\sum\limits_{k=0}^i \left|A_k\right|) + (-1)P(\sum\limits_{1 \leq k_1 \textless k_2 \leq i} \left|A_{k_1} \bigcap A_{k_2}\right|) + (-1)^2P(\sum\limits_{1 \leq k_1 \textless k_2 \textless k_3 \leq i} \left|A_{k_1} \bigcap A_{k_2} \bigcap A_{k_3}\right|) .. + (-1)^{i+1}P(\sum\limits_{1 \leq k_1 \textless k_2 \textless k_3 \textless .. k_i\leq i} \left|A_{k_1} \bigcap A_{k_2} \bigcap A_{k_3} ..\bigcap A_{k_i}\right|)

      Inclusion Exclusion principle and programming applications

      Sum Rule – If a task can be done in one of n_1 ways or one of n_2 ways, where none of the set of n_1 ways is the same as any of the set of n_2 ways, then there are n_1 + n_2 ways to do the task.
      The sum-rule mentioned above states that if there are multiple sets of ways of doing a task, there shouldn’t be any way that is common between two sets of ways because if there is, it would be counted twice and the enumeration would be wrong.
      The principle of inclusion-exclusion says that in order to count only unique ways of doing a task, we must add the number of ways to do it in one way and the number of ways to do it in another and then subtract the number of ways to do the task that are common to both sets of ways.
      The principle of inclusion-exclusion is also known as the subtraction principle. For two sets of ways A_1 and A_2, the enumeration would like-
      |A_1 \cup A_2| = |A_1| + |A_2| - |A_1\cap A_2|
      Below are some examples to explain the application of inclusion-exclusion principle:
      • Example 1: How many binary strings of length 8 either start with a ‘1’ bit or end with two bits ’00’?
        Solution: If the string starts with one, there are 7 characters left which can be filled in 2^7 = 128 ways.
        If the string ends with ’00’ then 6 characters can be filled in 2^6 = 64 ways.
        Now if we add the above sets of ways and conclude that it is the final answer, then it would be wrong. This is because there are strings with start with ‘1’ and end with ’00’ both, and since they satisfy both criteria they are counted twice.
        So we need to subtract such strings to get a correct count.
        Strings that start with ‘1’ and end with ’00’ have five characters that can be filled in 2^5 = 32 ways.
        So by the inclusion-exclusion principle we get-
        Total strings = 128 + 64 – 32 = 160
      • Example 2: How many numbers between 1 and 1000, including both, are divisible by 3 or 4?
        Solution: Number of numbers divisible by 3 = |A_1| =\lfloor 1000/3\rfloor = 333.
        Number of numbers divisible by 4 = |A_2| = \lfloor 1000/4\rfloor = 250.
        Number of numbers divisible by 3 and 4 = |A_1 \cap A_2| = \lfloor 1000/12\rfloor = 83.
        Therefore, number of numbers divisible by 3 or 4 = |A_1 \cup A_2| = 333 + 250 – 83 = 500