Graph Theory: Definitions for Common Terms

A graph is a data structure that is defined by two components :

A node or a vertex.
An edge E or ordered pair is a connection between two nodes u,v that is identified by unique pair(u,v). The pair (u,v) is ordered because (u,v) is not same as (v,u) in case of directed graph.The edge may have a weight or is set to one in case of unweighted graph.

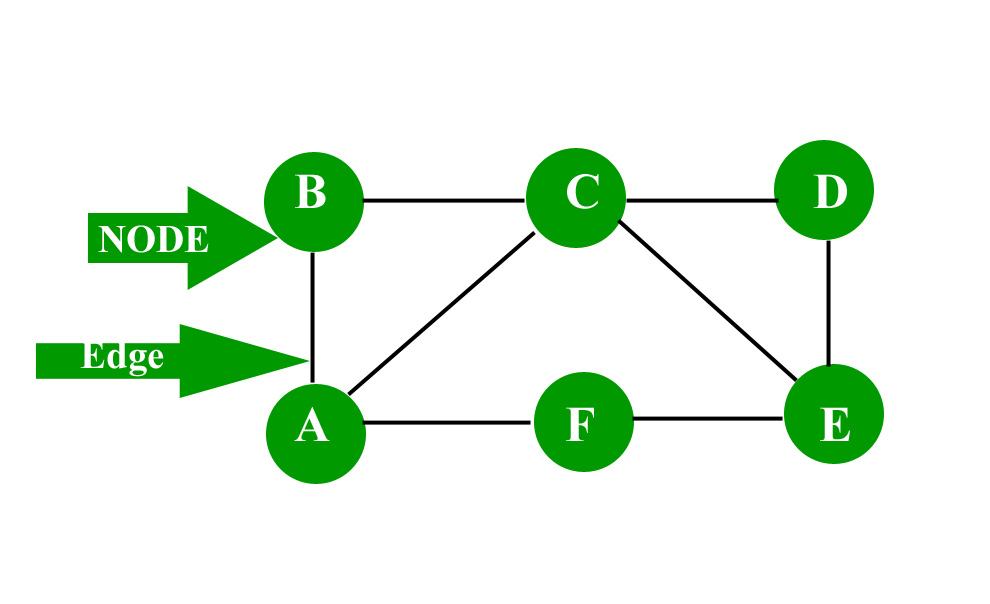
Consider the given below graph,
graph

Applications:

Graph is a data structure which is used extensively in our real-life.

Social Network: Each user is represented as a node and all their activities,suggestion and friend list are represented as an edge between the nodes.
Google Maps: Various locations are represented as vertices or nodes and the roads are represented as edges and graph theory is used to find shortest path between two nodes.
Recommendations on e-commerce websites: The “Recommendations for you” section on various e-commerce websites uses graph theory to recommend items of similar type to user’s choice.
Graph theory is also used to study molecules in chemistry and physics.

For more applications click here

More on graphs:
Characteristics of graphs:

Adjacent node: A node ‘v’ is said to be adjacent node of node ‘u’ if and only if there exists an edge between ‘u’ and ‘v’.
Degree of a node: In an undirected graph the number of nodes incident on a node is the degree of the node.
In case of directed graph ,Indegree of the node is the number of arriving edges to a node.
Outdegree of the node is the number of departing edges to a node.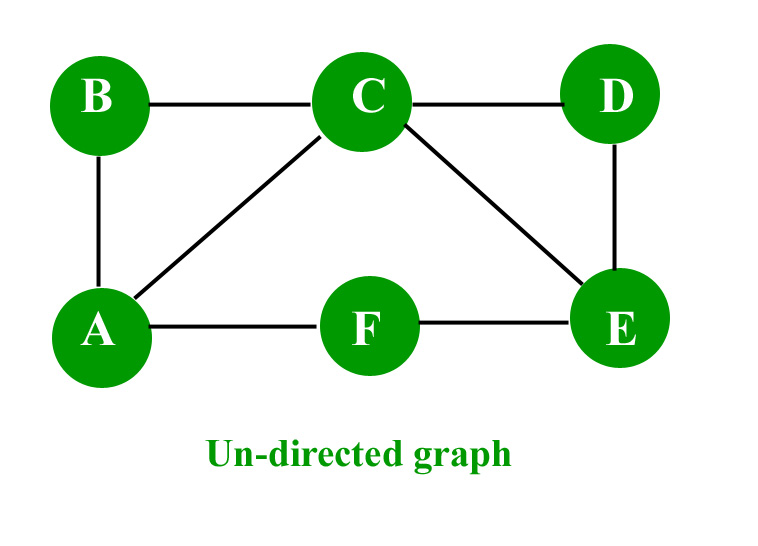
Path: A path of length ‘n’ from node ‘u’ to node ‘v’ is defined as sequence of n+1 nodes.
P(u,v)=(v0,v1,v2,v3…….vn)

A path is simple if all the nodes are distinct,exception is source and destination are same.
Isolated node: A node with degree 0 is known as isolated node.Isolated node can be found by Breadth first search(BFS). It finds its application in LAN network in finding whether a system is connected or not.

Types of graphs:

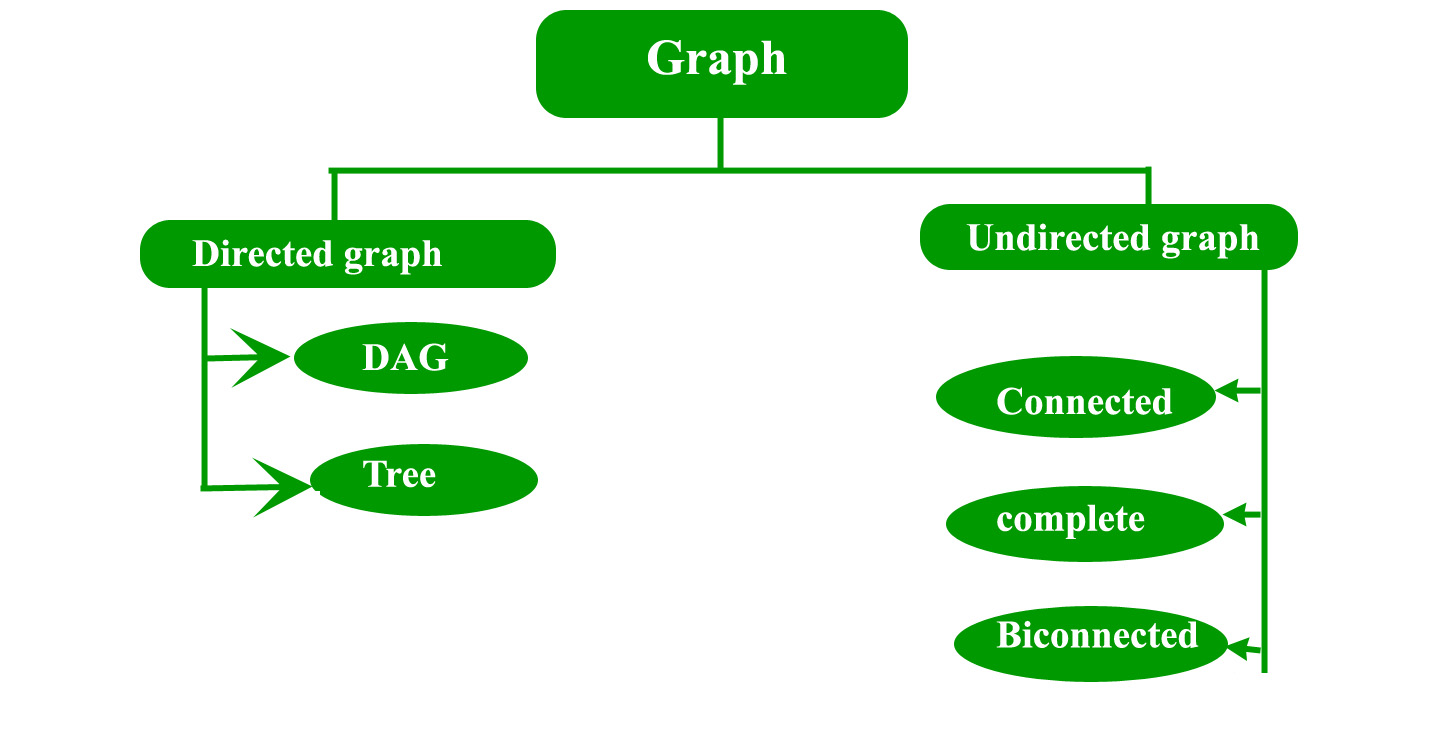
Directed graph:
A graph in which the direction of the edge is defined to a particular node is a directed graph.
- Directed Acyclic graph: It is a directed graph with no cycle.For a vertex ‘v’ in DAG there is no directed edge starting and ending with vertex ‘v’.
  a) Application :Critical game analysis,expression tree evaluation,game evaluation.
- Tree: A tree is just a restricted form of graph.That is, it is a DAG with a restriction that a child can have only one parent.
Undirected graph:
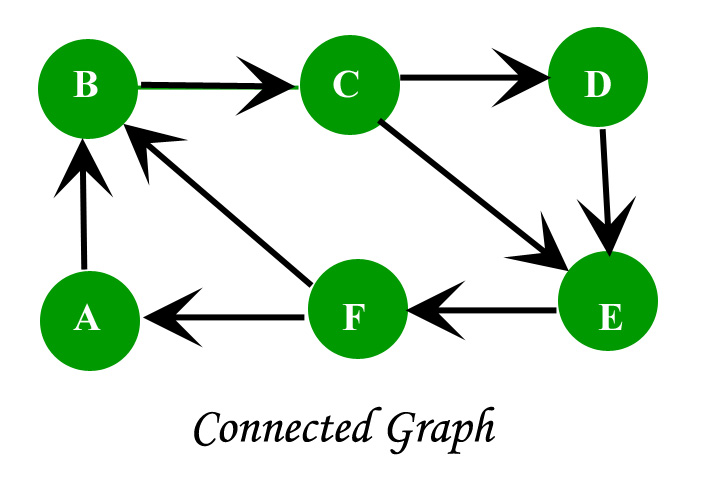
A graph in which the direction of the edge is not defined.So if an edge exists between node ‘u’ and ‘v’,then there is a path from node ‘u’ to ‘v’ and vice versa.
- Connected graph: A graph is connected when there is a path between every pair of vertices.In a connected graph there is no unreachable node.
- Complete graph: A graph in which each pair of graph vertices is connected by an edge.In other words,every node ‘u’ is adjacent to every other node ‘v’ in graph ‘G’.A complete graph would have n(n-1)/2 edges.See below for proof.
- Biconnected graph: A connected graph which cannot be broken down into any further pieces by deletion of any vertex.It is a graph with no articulation point.

Proof for complete graph:

Consider a complete graph with n nodes. Each node is connected to other n-1 nodes. Thus it becomes n * (n-1) edges. But this counts each edge twice because this is a undirected graph so divide it by 2.
Thus it becomes n(n-1)/2.

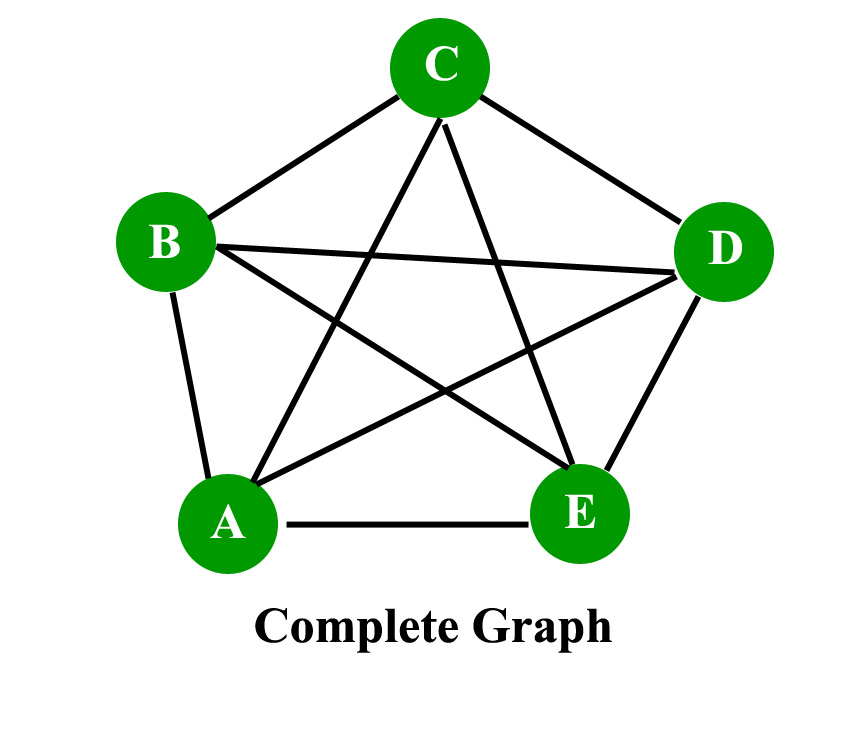
Consider the given graph,
//Omit the repetitive edges
Edges on node A = (A,B),(A,C),(A,E),(A,C).
Edges on node B = (B,C),(B,D),(B,E).
Edges on node C = (C,D),(C,E).
Edges on node D = (D,E).
Edges on node E = EMPTY.
Total edges = 4+3+2+1+0=10 edges.
Number of node = 5.
Thus n(n-1)/2=10 edges.
Thus proven.

A graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense “related”. The objects of the graph correspond to vertices and the relations between them correspond to edges. A graph is depicted diagrammatically as a set of dots depicting vertices connected by lines or curves depicting edges.
Formally,

“A graph $G = (V, E)$ consists of $V$ , a non-empty set of vertices (or nodes) and $E$ , a set of edges. Each edge has either one or two vertices associated with it, called its endpoints.”

Types of graph :There are several types of graphs distinguished on the basis of edges, their direction, their weight etc.

1. Simple graph – A graph in which each edge connects two different vertices and where no two edges connect the same pair of vertices is called a simple graph. For example, Consider the following graph –

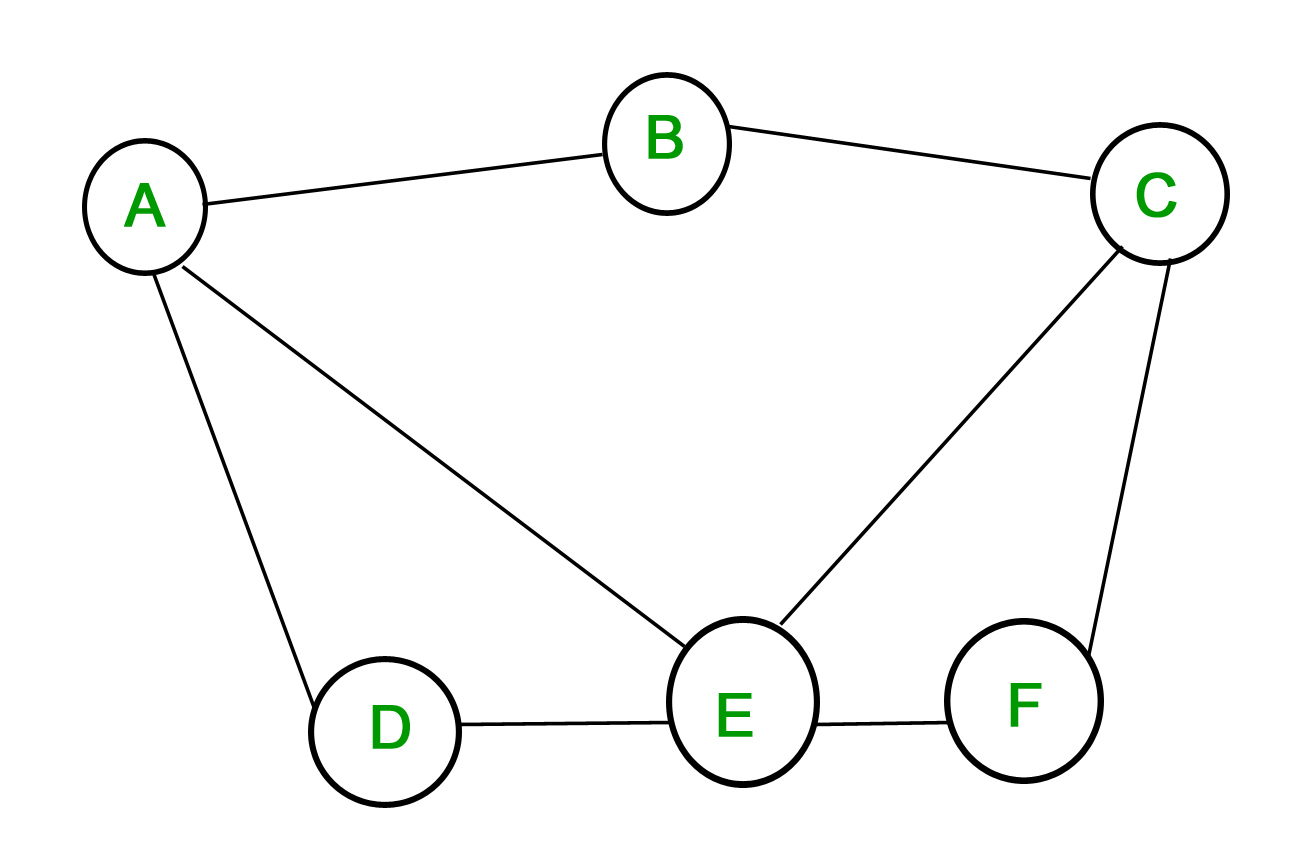
The above graph is a simple graph, since no vertex has a self-loop and no two vertices have more than one edge connecting them.
The edges are denoted by the vertices that they connect- $\{A,B\}$ is the edge connecting vertices $A$ and $B$ .

2. Multigraph – A graph in which multiple edges may connect the same pair of vertices is called a multigraph.
Since there can be multiple edges between the same pair of vertices, the multiplicity of edge tells the number of edges between two vertices.

The above graph is a multigraph since there are multiple edges between $B$ and $C$ . The multiplicity of the edge $\{B, C\}$ is 2.

In some graphs, unlike the one’s shown above, the edges are directed. This means that the relation between the objects is one-way only and not two-way. The direction of the edges may be important in some applications.

Based on whether the edges are directed or not we can have directed graphs and undirected graphs. This property can be extended to simple graphs and multigraphs to get simple directed or undirected simple graphs and directed or undirected multigraphs.

Basic graph Terminology :

In the above discussion some terms regarding graphs have already been explained such as vertices, edges, directed and undirected edges etc. There are more terms which describe properties of vertices and edges.

Adjacency – In a graph $G$ two vertices $u$ and $v$ are said to be adjacent if they are the endpoints of an edge. The edge $\{u, v\} - e$ is said to be incident with the vertices.
In case the edge is directed, $u$ is said to be adjacent to $v$ and $v$ is said to be adjacent from $u$ . Here, $u$ is said to be the intitial vertex and $v$ is said to the terminal vertex.
Degree – The degree of a vertex is the number of edges incident with it, except the self-loop which contributes twice to the degree of the vertex. Degree of a vertex $u$ is denoted as $deg(u)$ .
In case of directed graphs, the degree is further classified as in-degree and out-degree. The in-degree of a vertex is the number of edges with the given vertex as the terminal vertex. The out-degree of a vertex is the number of edges with the given vertex as the initial vertex. In-degree is denoted as $deg^-(u)$ and out-degree is denoted as $deg^+(u)$ .
For example in the directed graph shown above depicting flights between cities, the in-degree of the vertex “Delhi” is 3 and its out-degree is also 3.

Note: If a vertex has zero degree, it is called isolated. If the degree is one then it’s called pendant.

Handshaking Theorem :

What would one get if the degrees of all the vertices of a graph are added. In case of an undirected graph, each edge contributes twice, once for its initial vertex and second for its terminal vertex. So the sum of degrees is equal to twice the number of edges. This fact is stated in the Handshaking Theorem.

Let  be an undirected graph with  edges. Then


In case G is a directed graph,

An undirected graph has an even number of vertices of odd degree.

Proof : Let and be the sets of vertices of even and odd degrees respectively.
We know by the handshaking theorem that,

So,

The sum of degrees of vertices with even degrees is even. The LHS is also even, which means that the sum of degrees of vertices with odd degrees must be even.
Thus, the number of vertices with odd degree is even.

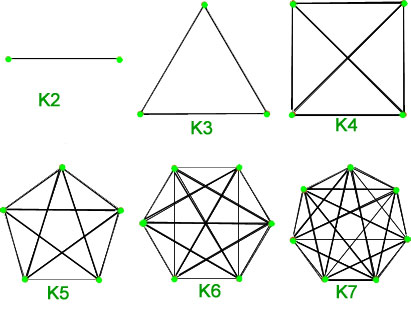
Some special Simple Graphs :

1. Complete Graphs – A simple graph of vertices having exactly one edge between each pair of vertices is called a complete graph. A complete graph of vertices is denoted by . Total number of edges are n*(n-1)/2 with n vertices in complete graph.

2. Cycles – Cycles are simple graphs with vertices and edges . Cycle with vertices is denoted as . Total number of edges are n with n vertices in cycle graph.

3. Wheels – A wheel is just like a cycle, with one additional vertex which is connected to every other vertex. Wheels of vertices with 1 addition vertex are denoted by . Total number of edges are 2*(n-1) with n vertices in wheel graph.

4. Hypercube – The Hypercube or n-cube is a graph with vertices each represented by a n-bit string. The vertices which differ by at most 1-bit are connected by edges. A hypercube of vertices is denoted by . Total number of edges are n* with vertices in cube graph.

5. Bipartite Graphs – A simple graph is said to be bipartite if its vertex set can be divided into two disjoint sets such that every edge in has its initial vertex in the first set and the terminal vertex in the second set. Total number of edges are (n*m) with (n+m) vertices in bipartite graph.

Theorem – A simple graph is bipartite if and only if it is possible to assign one of two
different colors to each vertex of the graph so that no two adjacent are assigned the
same color.

A bipartite graph with and vertices in its two disjoint subsets is said to be complete if there is an edge from every vertex in the first set to every vertex in the second set, for a total of edges. A complete bipartite graph with vertices in the first set and vertices in the second set is denoted as .