Net
Set operations
Introduction of Sets
A set is defined as a collection of distinct objects of the same type or class of objects. The purposes of a set are called elements or members of the set. An object can be numbers, alphabets, names, etc.
Examples of sets are:
- A set of rivers of India.
- A set of vowels.
We broadly denote a set by the capital letter A, B, C, etc. while the fundamentals of the set by small letter a, b, x, y, etc.
If A is a set, and a is one of the elements of A, then we denote it as a ∈ A. Here the symbol ∈ means -"Element of."
Sets Representation:
Sets are represented in two forms:-
a) Roster or tabular form: In this form of representation we list all the elements of the set within braces { } and separate them by commas.
Example: If A= set of all odd numbers less then 10 then in the roster from it can be expressed as A={ 1,3,5,7,9}.
b) Set Builder form: In this form of representation we list the properties fulfilled by all the elements of the set. We note as {x: x satisfies properties P}. and read as 'the set of those entire x such that each x has properties P.'
Example: If B= {2, 4, 8, 16, 32}, then the set builder representation will be: B={x: x=2n, where n ∈ N and 1≤ n ≥5}
Standard Notations:
| x ∈ A | x belongs to A or x is an element of set A. |
| x ∉ A | x does not belong to set A. |
| ∅ | Empty Set. |
| U | Universal Set. |
| N | The set of all natural numbers. |
| I | The set of all integers. |
| I0 | The set of all non- zero integers. |
| I+ | The set of all + ve integers. |
| C, C0 | The set of all complex, non-zero complex numbers respectively. |
| Q, Q0, Q+ | The sets of rational, non- zero rational, +ve rational numbers respectively. |
| R, R0, R+ | The set of real, non-zero real, +ve real number respectively. |
Cardinality of a Sets:
The total number of unique elements in the set is called the cardinality of the set. The cardinality of the countably infinite set is countably infinite.
Examples:
1. Let P = {k, l, m, n}
The cardinality of the set P is 4.
The cardinality of the set P is 4.
2. Let A is the set of all non-negative even integers, i.e.
A = {0, 2, 4, 6, 8, 10......}.
A = {0, 2, 4, 6, 8, 10......}.
As A is countably infinite set hence the cardinality.
Operations on Sets
The basic set operations are:
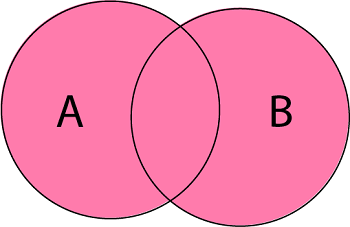
1. Union of Sets: Union of Sets A and B is defined to be the set of all those elements which belong to A or B or both and is denoted by A∪B.
Example: Let A = {1, 2, 3}, B= {3, 4, 5, 6}
A∪B = {1, 2, 3, 4, 5, 6}.
A∪B = {1, 2, 3, 4, 5, 6}.
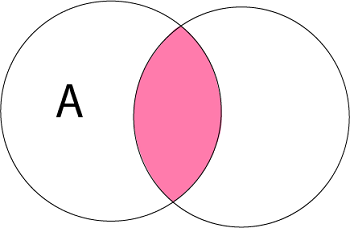
2. Intersection of Sets: Intersection of two sets A and B is the set of all those elements which belong to both A and B and is denoted by A ∩ B.
Example: Let A = {11, 12, 13}, B = {13, 14, 15}
A ∩ B = {13}.
A ∩ B = {13}.
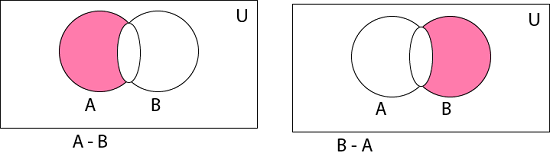
3. Difference of Sets: The difference of two sets A and B is a set of all those elements which belongs to A but do not belong to B and is denoted by A - B.
Example: Let A = {1, 2, 3, 4} and B = {3, 4, 5, 6} then A - B = {3, 4} and B - A = {5, 6}
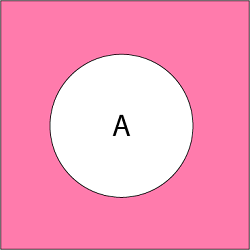
4. Complement of a Set: The Complement of a Set A is a set of all those elements of the universal set which do not belong to A and is denoted by Ac.
Ac = U - A = {x: x ∈ U and x ∉ A} = {x: x ∉ A}
Example: Let U is the set of all natural numbers.
A = {1, 2, 3}
Ac = {all natural numbers except 1, 2, and 3}.
A = {1, 2, 3}
Ac = {all natural numbers except 1, 2, and 3}.
5. Symmetric Difference of Sets: The symmetric difference of two sets A and B is the set containing all the elements that are in A or B but not in both and is denoted by A ⨁ B i.e.
Example: Let A = {a, b, c, d}
B = {a, b, l, m}
A ⨁ B = {c, d, l, m}
B = {a, b, l, m}
A ⨁ B = {c, d, l, m}
Algebra of Sets
Sets under the operations of union, intersection, and complement satisfy various laws (identities) which are listed in Table 1.
Table: Law of Algebra of Sets
| Idempotent Laws | (a) A ∪ A = A | (b) A ∩ A = A |
| Associative Laws | (a) (A ∪ B) ∪ C = A ∪ (B ∪ C) | (b) (A ∩ B) ∩ C = A ∩ (B ∩ C) |
| Commutative Laws | (a) A ∪ B = B ∪ A | (b) A ∩ B = B ∩ A |
| Distributive Laws | (a) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) | (b) A ∩ (B ∪ C) =(A ∩ B) ∪ (A ∩ C) |
| De Morgan's Laws | (a) (A ∪B)c=Ac∩ Bc | (b) (A ∩B)c=Ac∪ Bc |
| Identity Laws | (a) A ∪ ∅ = A (b) A ∪ U = U | (c) A ∩ U =A (d) A ∩ ∅ = ∅ |
| Complement Laws | (a) A ∪ Ac= U (b) A ∩ Ac= ∅ | (c) Uc= ∅ (d) ∅c = U |
| Involution Law | (a) (Ac)c = A |
Table 1 shows the law of algebra of sets.
Example 1: Prove Idempotent Laws:
Solution:
Since, B ⊂ A ∪ B, therefore A ⊂ A ∪ A Let x ∈ A ∪ A ⇒ x ∈ A or x ∈ A ⇒ x ∈ A ∴ A ∪ A ⊂ A As A ∪ A ⊂ A and A ⊂ A ∪ A ⇒ A =A ∪ A. Hence Proved.
Solution:
Since, A ∩ B ⊂ B, therefore A ∩ A ⊂ A Let x ∈ A ⇒ x ∈ A and x ∈ A ⇒ x ∈ A ∩ A ∴ A ⊂ A ∩ A As A ∩ A ⊂ A and A ⊂ A ∩ A ⇒ A = A ∩ A. Hence Proved.
Example 2: Prove Associative Laws:
Solution:
Let some x ∈ (A'∪ B) ∪ C ⇒ (x ∈ A or x ∈ B) or x ∈ C ⇒ x ∈ A or x ∈ B or x ∈ C ⇒ x ∈ A or (x ∈ B or x ∈ C) ⇒ x ∈ A or x ∈ B ∪ C ⇒ x ∈ A ∪ (B ∪ C). Similarly, if some x ∈ A ∪ (B ∪ C), then x ∈ (A ∪ B) ∪ C. Thus, any x ∈ A ∪ (B ∪ C) ⇔ x ∈ (A ∪ B) ∪ C. Hence Proved.
Solution:
Let some x ∈ A ∩ (B ∩ C) ⇒ x ∈ A and x ∈ B ∩ C ⇒ x ∈ A and (x ∈ B and x ∈ C) ⇒ x ∈ A and x ∈ B and x ∈ C ⇒ (x ∈ A and x ∈ B) and x ∈ C) ⇒ x ∈ A ∩ B and x ∈ C ⇒ x ∈ (A ∩ B) ∩ C. Similarly, if some x ∈ A ∩ (B ∩ C), then x ∈ (A ∩ B) ∩ C Thus, any x ∈ (A ∩ B) ∩ C ⇔ x ∈ A ∩ (B ∩ C). Hence Proved.
Example3: Prove Commutative Laws
Solution:
To Prove
A ∪ B = B ∪ A
A ∪ B = {x: x ∈ A or x ∈ B}
= {x: x ∈ B or x ∈ A} (∵ Order is not preserved in case of sets)
A ∪ B = B ∪ A. Hence Proved.
Solution:
To Prove
A ∩ B = B ∩ A
A ∩ B = {x: x ∈ A and x ∈ B}
= {x: x ∈ B and x ∈ A} (∵ Order is not preserved in case of sets)
A ∩ B = B ∩ A. Hence Proved.
Example 4: Prove Distributive Laws
Solution:
To Prove
Let x ∈ A ∪ (B ∩ C) ⇒ x ∈ A or x ∈ B ∩ C
⇒ (x ∈ A or x ∈ A) or (x ∈ B and x ∈ C)
⇒ (x ∈ A or x ∈ B) and (x ∈ A or x ∈ C)
⇒ x ∈ A ∪ B and x ∈ A ∪ C
⇒ x ∈ (A ∪ B) ∩ (A ∪ C)
Therefore, A ∪ (B ∩ C) ⊂ (A ∪ B) ∩ (A ∪ C)............(i)
Again, Let y ∈ (A ∪ B) ∩ (A ∪ C) ⇒ y ∈ A ∪ B and y ∈ A ∪ C
⇒ (y ∈ A or y ∈ B) and (y ∈ A or y ∈ C)
⇒ (y ∈ A and y ∈ A) or (y ∈ B and y ∈ C)
⇒ y ∈ A or y ∈ B ∩ C
⇒ y ∈ A ∪ (B ∩ C)
Therefore, (A ∪ B) ∩ (A ∪ C) ⊂ A ∪ (B ∩ C)............(ii)
Combining (i) and (ii), we get A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C). Hence Proved
Solution:
To Prove
Let x ∈ A ∩ (B ∪ C) ⇒ x ∈ A and x ∈ B ∪ C
⇒ (x ∈ A and x ∈ A) and (x ∈ B or x ∈ C)
⇒ (x ∈ A and x ∈ B) or (x ∈ A and x ∈ C)
⇒ x ∈ A ∩ B or x ∈ A ∩ C
⇒ x ∈ (A ∩ B) ∪ (A ∪ C)
Therefore, A ∩ (B ∪ C) ⊂ (A ∩ B) ∪ (A ∪ C)............ (i)
Again, Let y ∈ (A ∩ B) ∪ (A ∪ C) ⇒ y ∈ A ∩ B or y ∈ A ∩ C
⇒ (y ∈ A and y ∈ B) or (y ∈ A and y ∈ C)
⇒ (y ∈ A or y ∈ A) and (y ∈ B or y ∈ C)
⇒ y ∈ A and y ∈ B ∪ C
⇒ y ∈ A ∩ (B ∪ C)
Therefore, (A ∩ B) ∪ (A ∪ C) ⊂ A ∩ (B ∪ C)............ (ii)
Combining (i) and (ii), we get A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∪ C). Hence Proved
Example 5: Prove De Morgan's Laws
(a) (A ∪B)c=Ac∩ Bc
Solution:
To Prove (A ∪B)c=Ac∩ Bc
Let x ∈ (A ∪B)c ⇒ x ∉ A ∪ B (∵ a ∈ A ⇔ a ∉ Ac)
⇒ x ∉ A and x ∉ B
⇒ x ∉ Ac and x ∉ Bc
⇒ x ∉ Ac∩ Bc
Therefore, (A ∪B)c ⊂ Ac∩ Bc............. (i)
Again, let x ∈ Ac∩ Bc ⇒ x ∈ Ac and x ∈ Bc
⇒ x ∉ A and x ∉ B
⇒ x ∉ A ∪ B
⇒ x ∈ (A ∪B)c
Therefore, Ac∩ Bc ⊂ (A ∪B)c............. (ii)
Combining (i) and (ii), we get Ac∩ Bc =(A ∪B)c. Hence Proved.
(b) (A ∩B)c = Ac∪ Bc
Solution:
Let x ∈ (A ∩B)c ⇒ x ∉ A ∩ B (∵ a ∈ A ⇔ a ∉ Ac)
⇒ x ∉ A or x ∉ B
⇒ x ∈ Ac and x ∈ Bc
⇒ x ∈ Ac∪ Bc
∴ (A ∩B)c⊂ (A ∪B)c.................. (i)
Again, Let x ∈ Ac∪ Bc ⇒ x ∈ Ac or x ∈ Bc
⇒ x ∉ A or x ∉ B
⇒ x ∉ A ∩ B
⇒ x ∈ (A ∩B)c
∴ Ac∪ Bc⊂ (A ∩B)c.................... (ii)
Combining (i) and (ii), we get(A ∩B)c=Ac∪ Bc. Hence Proved.
Example 6: Prove Identity Laws.
Solution:
To Prove A ∪ ∅ = A
Let x ∈ A ∪ ∅ ⇒ x ∈ A or x ∈ ∅
⇒ x ∈ A (∵x ∈ ∅, as ∅ is the null set )
Therefore, x ∈ A ∪ ∅ ⇒ x ∈ A
Hence, A ∪ ∅ ⊂ A.
We know that A ⊂ A ∪ B for any set B.
But for B = ∅, we have A ⊂ A ∪ ∅
From above, A ⊂ A ∪ ∅ , A ∪ ∅ ⊂ A ⇒ A = A ∪ ∅. Hence Proved.
Solution:
To Prove A ∩ ∅ = ∅ If x ∈ A, then x ∉ ∅ (∵∅ is a null set) Therefore, x ∈ A, x ∉ ∅ ⇒ A ∩ ∅ = ∅. Hence Proved.
Solution:
To Prove A ∪ U = U
Every set is a subset of a universal set.
∴ A ∪ U ⊆ U
Also, U ⊆ A ∪ U
Therefore, A ∪ U = U. Hence Proved.
Solution:
To Prove A ∩ U = A We know A ∩ U ⊂ A................. (i) So we have to show that A ⊂ A ∩ U Let x ∈ A ⇒ x ∈ A and x ∈ U (∵ A ⊂ U so x ∈ A ⇒ x ∈ U ) ∴ x ∈ A ⇒ x ∈ A ∩ U ∴ A ⊂ A ∩ U................. (ii) From (i) and (ii), we get A ∩ U = A. Hence Proved.
Example7: Prove Complement Laws
(a) A ∪ Ac= U
Solution:
To Prove A ∪ Ac= U
Every set is a subset of U
∴ A ∪ Ac ⊂ U.................. (i)
We have to show that U ⊆ A ∪ Ac
Let x ∈ U ⇒ x ∈ A or x ∉ A
⇒ x ∈ A or x ∈ Ac ⇒ x ∈ A ∪ Ac
∴ U ⊆ A ∪ Ac................... (ii)
From (i) and (ii), we get A ∪ Ac= U. Hence Proved.
(b) A ∩ Ac=∅
Solution:
As ∅ is the subset of every set
∴ ∅ ⊆ A ∩ Ac..................... (i)
We have to show that A ∩ Ac ⊆ ∅
Let x ∈ A ∩ Ac ⇒ x ∈ A and x ∈ Ac
⇒ x ∈ A and x ∉ A
⇒ x ∈ ∅
∴ A ∩ Ac ⊂∅..................... (ii)
From (i) and (ii), we get A∩ Ac=∅. Hence Proved.
(c) Uc= ∅
Solution:
Let x ∈ Uc ⇔ x ∉ U ⇔ x ∈ ∅
∴ Uc= ∅. Hence Proved. (As U is the Universal Set).
(d) ∅c = U
Solution:
Let x ∈ ∅c ⇔ x ∉ ∅ ⇔ x ∈ U (As ∅ is an empty set) ∴ ∅c = U. Hence Proved.
Example8: Prove Involution Law
(a) (Ac )c A.
Solution:
Let x ∈ (Ac )c ⇔ x ∉ Ac⇔ x ∈ a
∴ (Ac )c =A. Hence Proved.
Duality:
The dual E∗ of E is the equation obtained by replacing every occurrence of ∪, ∩, U and ∅ in E by ∩, ∪, ∅, and U, respectively. For example, the dual of
It is noted as the principle of duality, that if any equation E is an identity, then its dual E∗ is also an identity.
Principle of Extension:
According to the Principle of Extension two sets, A and B are the same if and only if they have the same members. We denote equal sets by A=B.
Cartesian product of two sets:
The Cartesian Product of two sets P and Q in that order is the set of all ordered pairs whose first member belongs to the set P and second member belong to set Q and is denoted by P x Q, i.e.,
Example: Let P = {a, b, c} and Q = {k, l, m, n}. Determine the Cartesian product of P and Q.
Solution: The Cartesian product of P and Q is
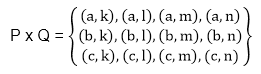
Multisets
A multiset is an unordered collection of elements, in which the multiplicity of an element may be one or more than one or zero. The multiplicity of an element is the number of times the element repeated in the multiset. In other words, we can say that an element can appear any number of times in a set.
Example:
Operations on Multisets
1. Union of Multisets: The Union of two multisets A and B is a multiset such that the multiplicity of an element is equal to the maximum of the multiplicity of an element in A and B and is denoted by A ∪ B.
Example:
2. Intersections of Multisets: The intersection of two multisets A and B, is a multiset such that the multiplicity of an element is equal to the minimum of the multiplicity of an element in A and B and is denoted by A ∩ B.
Example:
3. Difference of Multisets: The difference of two multisets A and B, is a multiset such that the multiplicity of an element is equal to the multiplicity of the element in A minus the multiplicity of the element in B if the difference is +ve, and is equal to 0 if the difference is 0 or negative
Example:
4. Sum of Multisets: The sum of two multisets A and B, is a multiset such that the multiplicity of an element is equal to the sum of the multiplicity of an element in A and B
Example:
5. Cardinality of Sets: The cardinality of a multiset is the number of distinct elements in a multiset without considering the multiplicity of an element
Example:
The cardinality of the multiset A is 5.
Ordered Set
It is defined as the ordered collection of distinct objects.
Example:
Ordered Pairs
An Ordered Pair consists of two elements such that one of them is designated as the first member and other as the second member.
(a, b) and (b, a) are two different ordered pair. An ordered triple can also be written regarding an ordered pair as {(a, b) c}
An ordered Quadrable is an ordered pair {(((a, b), c) d)} with the first element as ordered triple.
An ordered n-tuple is an ordered pair where the first component is an ordered (n - 1) tuples, and the nth element is the second component.
Example:
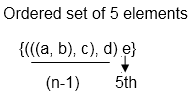
Enclusion-Exclusion Principle
Let A, B be any two finite sets. Then n (A ∪ B) = n (A) + n (B) - n (A ∩ B)
Here "include" n (A) and n (B) and we "exclude" n (A ∩ B)
Example 1:
Suppose A, B, C are finite sets. Then A ∪ B ∪ C is finite and n (A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n(B ∩ C) + n(A ∩ B ∩ C)
Example 2:
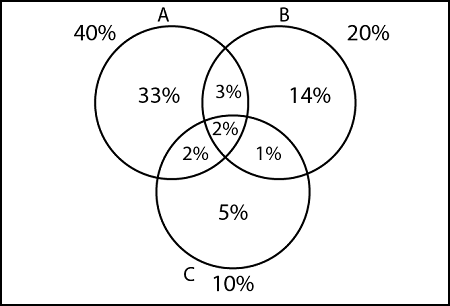
In a town of 10000 families it was found that 40% of families buy newspaper A, 20% family buy newspaper B, 10% family buy newspaper C, 5% family buy newspaper A and B, 3% family buy newspaper B and C and 4% family buy newspaper A and C. If 2% family buy all the newspaper. Find the number of families which buy
- Number of families which buy all three newspapers.
- Number of families which buy newspaper A only
- Number of families which buy newspaper B only
- Number of families which buy newspaper C only
- Number of families which buy None of A, B, C
- Number of families which buy exactly only one newspaper
- Number of families which buy newspaper A and B only
- Number of families which buy newspaper B and C only
- Number of families which buy newspaper C and A only
- Number of families which buy at least two newspapers
- Number of families which buy at most two newspapers
- Number of families which buy exactly two newspapers
Solution:
1. Number of families which buy all three newspapers:
2. Number of families which buy newspaper A only
3. Number of families which buy newspaper B only
4. Number of families which buy newspaper C only
5. Number of families which buy None of A, B, and C
n (A ∪B ∪C)c = 100 - n (A ∪ B ∪ C) n (A ∪B ∪C)c = 100 - [40 + 20 + 10 - 5- 3- 4 + 2] n (A ∪B ∪C)c = 100 - 60 = 40 %
6. Number of families which buy exactly only one newspaper
7. Number of families which buy newspaper A and B only
8. Number of families which buy newspaper B and C only
9. Number of families which buy newspaper C and A only
10. Number of families which buy at least two newspapers
11. Number of families which buy at most two newspapers
12. Number of families which buy exactly two newspapers

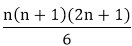
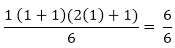 = 1
= 1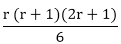 is true........... (ii)
is true........... (ii)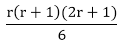 + (r+1)2
+ (r+1)2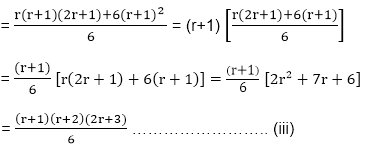
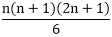 is true for n = 1, 2, 3, 4, 5 ..... Hence Proved.
is true for n = 1, 2, 3, 4, 5 ..... Hence Proved.