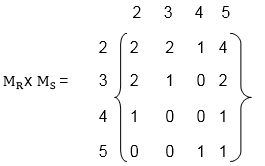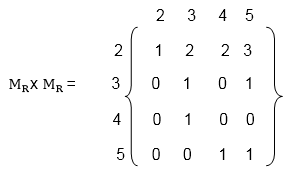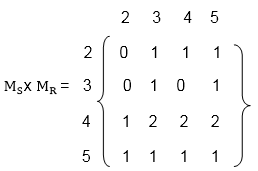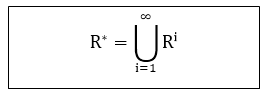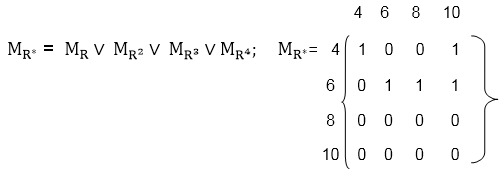Let P and Q be two non- empty sets. A binary relation R is defined to be a subset of P x Q from a set P to Q. If (a, b) ∈ R and R ⊆ P x Q then a is related to b by R i.e., aRb. If sets P and Q are equal, then we say R ⊆ P x P is a relation on P e.g.
Consider a relation R from a set A to set B. The complement of relation R denoted by R is a relation from A to B such that
X x Y = {(1, 8), (2, 8), (3, 8), (1, 9), (2, 9), (3, 9)}
Now we find the complement relation R from X x Y
R = {(3, 8), (2, 9)}
Representation of Relations
Relations can be represented in many ways. Some of which are as follows:
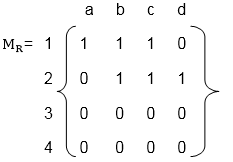
1. Relation as a Matrix: Let P = [a1,a2,a3,.......am] and Q = [b1,b2,b3......bn] are finite sets, containing m and n number of elements respectively. R is a relation from P to Q. The relation R can be represented by m x n matrix M = [Mij], defined as
Mij = 0 if (ai,bj) ∉ R
1 if (ai,bj )∈ R
Example
- Let P = {1, 2, 3, 4}, Q = {a, b, c, d}
- and R = {(1, a), (1, b), (1, c), (2, b), (2, c), (2, d)}.
The matrix of relation R is shown as fig:
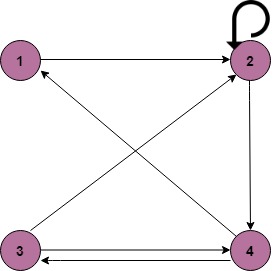
2. Relation as a Directed Graph: There is another way of picturing a relation R when R is a relation from a finite set to itself.
Example
- A = {1, 2, 3, 4}
- R = {(1, 2) (2, 2) (2, 4) (3, 2) (3, 4) (4, 1) (4, 3)}
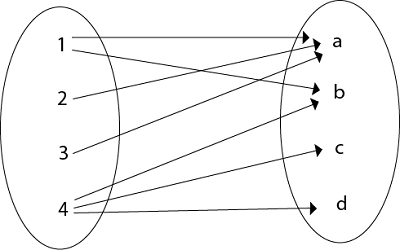
3. Relation as an Arrow Diagram: If P and Q are finite sets and R is a relation from P to Q. Relation R can be represented as an arrow diagram as follows.
Draw two ellipses for the sets P and Q. Write down the elements of P and elements of Q column-wise in three ellipses. Then draw an arrow from the first ellipse to the second ellipse if a is related to b and a ∈ P and b ∈ Q.
Example
- Let P = {1, 2, 3, 4}
- Q = {a, b, c, d}
- R = {(1, a), (2, a), (3, a), (1, b), (4, b), (4, c), (4, d)
The arrow diagram of relation R is shown in fig:
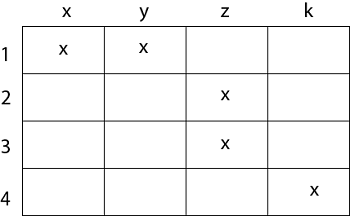
4. Relation as a Table: If P and Q are finite sets and R is a relation from P to Q. Relation R can be represented in tabular form.
Make the table which contains rows equivalent to an element of P and columns equivalent to the element of Q. Then place a cross (X) in the boxes which represent relations of elements on set P to set Q.
Example
- Let P = {1, 2, 3, 4}
- Q = {x, y, z, k}
- R = {(1, x), (1, y), (2, z), (3, z), (4, k)}.
The tabular form of relation as shown in fig:
Composition of Relations
Let A, B, and C be sets, and let R be a relation from A to B and let S be a relation from B to C. That is, R is a subset of A × B and S is a subset of B × C. Then R and S give rise to a relation from A to C indicated by R◦S and defined by:
- a (R◦S)c if for some b ∈ B we have aRb and bSc.
- is,
- R ◦ S = {(a, c)| there exists b ∈ B for which (a, b) ∈ R and (b, c) ∈ S}
The relation R◦S is known the composition of R and S; it is sometimes denoted simply by RS.
Let R is a relation on a set A, that is, R is a relation from a set A to itself. Then R◦R, the composition of R with itself, is always represented. Also, R◦R is sometimes denoted by R2. Similarly, R3 = R2◦R = R◦R◦R, and so on. Thus Rn is defined for all positive n.
Example1: Let X = {4, 5, 6}, Y = {a, b, c} and Z = {l, m, n}. Consider the relation R1 from X to Y and R2 from Y to Z.
R1 = {(4, a), (4, b), (5, c), (6, a), (6, c)}
R2 = {(a, l), (a, n), (b, l), (b, m), (c, l), (c, m), (c, n)}
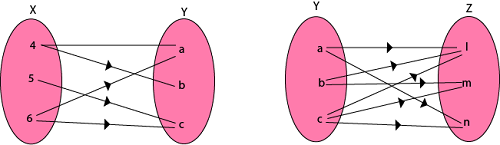
Find the composition of relation (i) R1 o R2 (ii) R1o R1-1
Solution:
(i) The composition relation R1 o R2 as shown in fig:
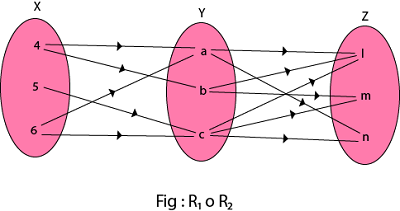
R1 o R2 = {(4, l), (4, n), (4, m), (5, l), (5, m), (5, n), (6, l), (6, m), (6, n)}
(ii) The composition relation R1o R1-1 as shown in fig:
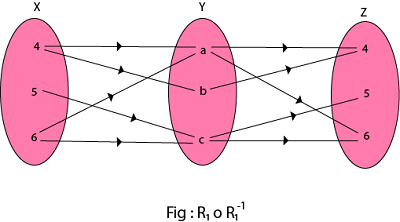
R1o R1-1 = {(4, 4), (5, 5), (5, 6), (6, 4), (6, 5), (4, 6), (6, 6)}
Composition of Relations and Matrices
There is another way of finding R◦S. Let MR and MS denote respectively the matrix representations of the relations R and S. Then
Example
- Let P = {2, 3, 4, 5}. Consider the relation R and S on P defined by
- R = {(2, 2), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5), (5, 3)}
- S = {(2, 3), (2, 5), (3, 4), (3, 5), (4, 2), (4, 3), (4, 5), (5, 2), (5, 5)}.
-
- Find the matrices of the above relations.
- Use matrices to find the following composition of the relation R and S.
- (i)RoS (ii)RoR (iii)SoR
Solution: The matrices of the relation R and S are a shown in fig:
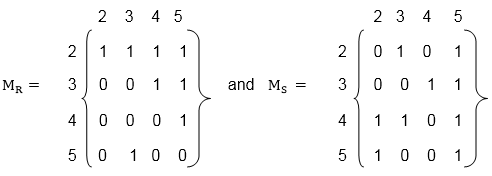
(i) To obtain the composition of relation R and S. First multiply MR with MS to obtain the matrix MR x MS as shown in fig:
The non zero entries in the matrix MR x MS tells the elements related in RoS. So,
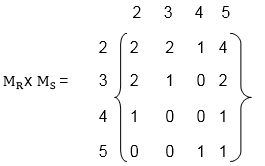
Hence the composition R o S of the relation R and S is
- R o S = {(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (4, 2), (4, 5), (5, 2), (5, 3), (5, 4), (5, 5)}.
(ii) First, multiply the matrix MR by itself, as shown in fig
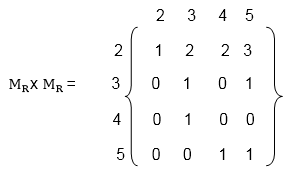
Hence the composition R o R of the relation R and S is
- R o R = {(2, 2), (3, 2), (3, 3), (3, 4), (4, 2), (4, 5), (5, 2), (5, 3), (5, 5)}
(iii) Multiply the matrix MS with MR to obtain the matrix MS x MR as shown in fig:
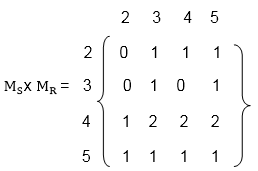
The non-zero entries in matrix MS x MR tells the elements related in S o R.
Hence the composition S o R of the relation S and R is
- S o R = {(2, 4) , (2, 5), (3, 3), (3, 4), (3, 5), (4, 2), (4, 4), (4, 5), (5, 2), (5, 3), (5, 4), (5, 5)}.
Types of Relations
1. Reflexive Relation: A relation R on set A is said to be a reflexive if (a, a) ∈ R for every a ∈ A.
Example: If A = {1, 2, 3, 4} then R = {(1, 1) (2, 2), (1, 3), (2, 4), (3, 3), (3, 4), (4, 4)}. Is a relation reflexive?
Solution: The relation is reflexive as for every a ∈ A. (a, a) ∈ R, i.e. (1, 1), (2, 2), (3, 3), (4, 4) ∈ R.
2. Irreflexive Relation: A relation R on set A is said to be irreflexive if (a, a) ∉ R for every a ∈ A.
Example: Let A = {1, 2, 3} and R = {(1, 2), (2, 2), (3, 1), (1, 3)}. Is the relation R reflexive or irreflexive?
Solution: The relation R is not reflexive as for every a ∈ A, (a, a) ∉ R, i.e., (1, 1) and (3, 3) ∉ R. The relation R is not irreflexive as (a, a) ∉ R, for some a ∈ A, i.e., (2, 2) ∈ R.
3. Symmetric Relation: A relation R on set A is said to be symmetric iff (a, b) ∈ R ⟺ (b, a) ∈ R.
Example: Let A = {1, 2, 3} and R = {(1, 1), (2, 2), (1, 2), (2, 1), (2, 3), (3, 2)}. Is a relation R symmetric or not?
Solution: The relation is symmetric as for every (a, b) ∈ R, we have (b, a) ∈ R, i.e., (1, 2), (2, 1), (2, 3), (3, 2) ∈ R but not reflexive because (3, 3) ∉ R.
Example of Symmetric Relation:
- Relation ⊥r is symmetric since a line a is ⊥r to b, then b is ⊥r to a.
- Also, Parallel is symmetric, since if a line a is ∥ to b then b is also ∥ to a.
Antisymmetric Relation: A relation R on a set A is antisymmetric iff (a, b) ∈ R and (b, a) ∈ R then a = b.
Example1: Let A = {1, 2, 3} and R = {(1, 1), (2, 2)}. Is the relation R antisymmetric?
Solution: The relation R is antisymmetric as a = b when (a, b) and (b, a) both belong to R.
Example2: Let A = {4, 5, 6} and R = {(4, 4), (4, 5), (5, 4), (5, 6), (4, 6)}. Is the relation R antisymmetric?
Solution: The relation R is not antisymmetric as 4 ≠ 5 but (4, 5) and (5, 4) both belong to R.
5. Asymmetric Relation: A relation R on a set A is called an Asymmetric Relation if for every (a, b) ∈ R implies that (b, a) does not belong to R.
6. Transitive Relations: A Relation R on set A is said to be transitive iff (a, b) ∈ R and (b, c) ∈ R ⟺ (a, c) ∈ R.
Example1: Let A = {1, 2, 3} and R = {(1, 2), (2, 1), (1, 1), (2, 2)}. Is the relation transitive?
Solution: The relation R is transitive as for every (a, b) (b, c) belong to R, we have (a, c) ∈ R i.e, (1, 2) (2, 1) ∈ R ⇒ (1, 1) ∈ R.
Note1: The Relation ≤, ⊆ and / are transitive, i.e., a ≤ b, b ≤ c then a ≤ c
(ii) Let a ⊆ b, b ⊆ c then a ⊆ c
(iii) Let a/b, b/c then a/c.
Note2: ⊥r is not transitive since a ⊥r b, b ⊥r c then it is not true that a ⊥r c. Since no line is ∥ to itself, we can have a ∥ b, b ∥ a but a ∦ a.
Thus ∥ is not transitive, but it will be transitive in the plane.
7. Identity Relation: Identity relation I on set A is reflexive, transitive and symmetric. So identity relation I is an Equivalence Relation.
Example: A= {1, 2, 3} = {(1, 1), (2, 2), (3, 3)}
8. Void Relation: It is given by R: A →B such that R = ∅ (⊆ A x B) is a null relation. Void Relation R = ∅ is symmetric and transitive but not reflexive.
9. Universal Relation: A relation R: A →B such that R = A x B (⊆ A x B) is a universal relation. Universal Relation from A →B is reflexive, symmetric and transitive. So this is an equivalence relation.
Closure Properties of Relations
Consider a given set A, and the collection of all relations on A. Let P be a property of such relations, such as being symmetric or being transitive. A relation with property P will be called a P-relation. The P-closure of an arbitrary relation R on A, indicated P (R), is a P-relation such that
(1) Reflexive and Symmetric Closures: The next theorem tells us how to obtain the reflexive and symmetric closures of a relation easily.
Theorem: Let R be a relation on a set A. Then:
- R ∪ ∆A is the reflexive closure of R
- R ∪ R-1 is the symmetric closure of R.
Example1:
- Let A = {k, l, m}. Let R is a relation on A defined by
- R = {(k, k), (k, l), (l, m), (m, k)}.
Find the reflexive closure of R.
Solution: R ∪ ∆ is the smallest relation having reflexive property, Hence,
RF = R ∪ ∆ = {(k, k), (k, l), (l, l), (l, m), (m, m), (m, k)}.
Example2: Consider the relation R on A = {4, 5, 6, 7} defined by
- R = {(4, 5), (5, 5), (5, 6), (6, 7), (7, 4), (7, 7)}
Find the symmetric closure of R.
Solution: The smallest relation containing R having the symmetric property is R ∪ R-1,i.e.
RS = R ∪ R-1 = {(4, 5), (5, 4), (5, 5), (5, 6), (6, 5), (6, 7), (7, 6), (7, 4), (4, 7), (7, 7)}.
(2)Transitive Closures: Consider a relation R on a set A. The transitive closure R of a relation R of a relation R is the smallest transitive relation containing R.
Recall that R2 = R◦ R and Rn = Rn-1 ◦ R. We define
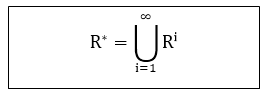
The following Theorem applies:
Theorem1: R* is the transitive closure of R
Suppose A is a finite set with n elements.
Theorem 2: Let R be a relation on a set A with n elements. Then
Transitive (R) = R ∪ R2∪.....∪ Rn
Example1: Consider the relation R = {(1, 2), (2, 3), (3, 3)} on A = {1, 2, 3}. Then
R2 = R◦ R = {(1, 3), (2, 3), (3, 3)} and R3 = R2 ◦ R = {(1, 3), (2, 3), (3, 3)} Accordingly,
Transitive (R) = {(1, 2), (2, 3), (3, 3), (1, 3)}
Example2: Let A = {4, 6, 8, 10} and R = {(4, 4), (4, 10), (6, 6), (6, 8), (8, 10)} is a relation on set A. Determine transitive closure of R.
Solution: The matrix of relation R is shown in fig:
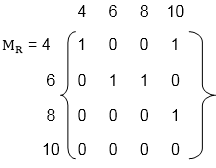
Now, find the powers of MR as in fig:
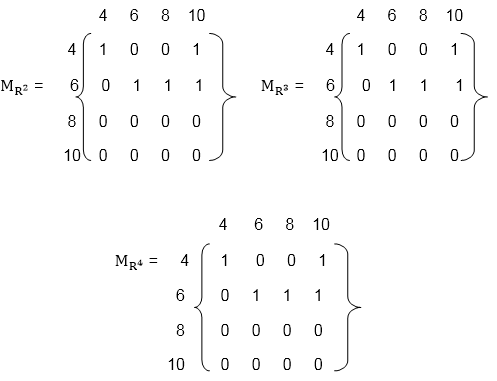
Hence, the transitive closure of MR is MR* as shown in Fig (where MR* is the ORing of a power of MR).
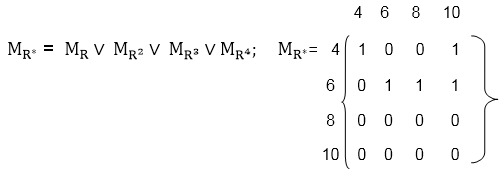
Thus, R* = {(4, 4), (4, 10), (6, 8), (6, 6), (6, 10), (8, 10)}.
Note: While ORing the power of the matrix R, we can eliminate MRn because it is equal to MR* if n is even and is equal to MR3 if n is odd.
 2. Relation as a Directed Graph: There is another way of picturing a relation R when R is a relation from a finite set to itself.Example
2. Relation as a Directed Graph: There is another way of picturing a relation R when R is a relation from a finite set to itself.Example 3. Relation as an Arrow Diagram: If P and Q are finite sets and R is a relation from P to Q. Relation R can be represented as an arrow diagram as follows.Draw two ellipses for the sets P and Q. Write down the elements of P and elements of Q column-wise in three ellipses. Then draw an arrow from the first ellipse to the second ellipse if a is related to b and a ∈ P and b ∈ Q.ExampleThe arrow diagram of relation R is shown in fig:
3. Relation as an Arrow Diagram: If P and Q are finite sets and R is a relation from P to Q. Relation R can be represented as an arrow diagram as follows.Draw two ellipses for the sets P and Q. Write down the elements of P and elements of Q column-wise in three ellipses. Then draw an arrow from the first ellipse to the second ellipse if a is related to b and a ∈ P and b ∈ Q.ExampleThe arrow diagram of relation R is shown in fig: 4. Relation as a Table: If P and Q are finite sets and R is a relation from P to Q. Relation R can be represented in tabular form.Make the table which contains rows equivalent to an element of P and columns equivalent to the element of Q. Then place a cross (X) in the boxes which represent relations of elements on set P to set Q.ExampleThe tabular form of relation as shown in fig:
4. Relation as a Table: If P and Q are finite sets and R is a relation from P to Q. Relation R can be represented in tabular form.Make the table which contains rows equivalent to an element of P and columns equivalent to the element of Q. Then place a cross (X) in the boxes which represent relations of elements on set P to set Q.ExampleThe tabular form of relation as shown in fig: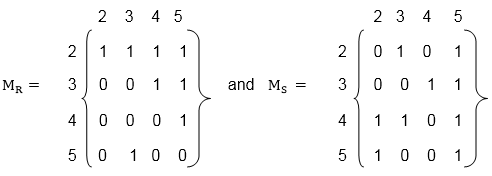 (i) To obtain the composition of relation R and S. First multiply MR with MS to obtain the matrix MR x MS as shown in fig:The non zero entries in the matrix MR x MS tells the elements related in RoS. So,Hence the composition R o S of the relation R and S is(ii) First, multiply the matrix MR by itself, as shown in figHence the composition R o R of the relation R and S is(iii) Multiply the matrix MS with MR to obtain the matrix MS x MR as shown in fig:The non-zero entries in matrix MS x MR tells the elements related in S o R.Hence the composition S o R of the relation S and R is
(i) To obtain the composition of relation R and S. First multiply MR with MS to obtain the matrix MR x MS as shown in fig:The non zero entries in the matrix MR x MS tells the elements related in RoS. So,Hence the composition R o S of the relation R and S is(ii) First, multiply the matrix MR by itself, as shown in figHence the composition R o R of the relation R and S is(iii) Multiply the matrix MS with MR to obtain the matrix MS x MR as shown in fig:The non-zero entries in matrix MS x MR tells the elements related in S o R.Hence the composition S o R of the relation S and R is